It’s now one of the most widely-used ways to understand behaviour and everyone from academic psychologists to business leaders rely on it for insights and predictions.
What is the concept of game theory?
Game theory is the study of mathematical models of behaviour among rational decision-makers. At least, that’s the definition Wikipedia gives. Trouble is, it’s kind of dry. I don’t feel like I’m any the wiser after reading it.
Game theory is the idea that interactions — diplomacy, corporate takeovers, traffic on a bridge or two people in a room — can be understood as a game. We can build a game that works as a model of the interaction, then use that model to understand what people are likely to do in that situation.
Phrased this way, game theory sounds quite lightweight. And it has the advantage that the concepts it generates are often quite easy to explain to non-experts. But the maths it’s based on is seriously heavyweight.
Game theory was initially developed by John von Neumann, widely regarded as the best mathematician of his time and a major contribution to quantum mechanics, computing, pure mathematics, statistics, and every other subject mathematics touches. His original paper on game theory was highly abstruse, essentially a pure mathematical work. But soon people from all sorts of disciplines expanded the original game theory, which dealt only with zero-sum games (see below), into a complete system for understanding complex interactions.
What kinds of games are used in game theory?
Game theory originally used only zero-sum games. A zero-sum game is one in which one participant gets everything, the other nothing; think of chess: you win completely, or lose completely. You can draw, true, but you can’t 75% win. It’s either-or. Zero-sum games can also be those in which one player’s losses are another’s winnings; poker can have several winners and several losers, but the pool of winnings is taken from the losers in the form of bets so it’s seen as a zero-sum game.
Other zero-sum games include futures and options in the financial market: they’re a bet between investors, and when one wins, the other loses.
Non-zero-sum games are more common. These are games in which the system as a whole benefits from the actions of all participants, such as where competing firms collaborate, knowingly or through the Invisible Hand, to expand their industry or market. When Levis make jeans look cool, Wranglers also profits.
Another type of non-zero-sum game is one in which the participants are adversarial but the payoffs are asymmetrical. For instance, pirates and traders: a win for the pirates involves robbing the traders, while a win for the traders involves fighting off the pirates, but no additional profit. This scenario is the same for cybersecurity, asset custody and so on; all are non-zero-sum games.
One of the most famous examples of game theory in action is also among the easiest to understand, as well as one of the more sophisticated examples: the prisoner’s dilemma.
What is the Prisoner’s Dilemma?
The prisoner’s dilemma is a game in which the participants have a zero-sum incentive to harm each other and non-zero-sum incentive not to harm each other. It’s conceived as a thought experiment, based on work by Melvin Flood and Merril Dresher, and named and codified by Alfred Tucker. It’s technically a two-person non-cooperative variable-sum game, and it works like this:
Two members of a criminal gang have been arrested and are being kept in seperate cells, with no means of communicating with each other. Prosecutors know both are guilty of a major charge but have only enough evidence to convict on a much smaller charge. Each prisoner is given the offer: testify that both are guilty and be released, while the other is imprisoned on the major charge.
The incentives here are made more complex by the fact that the other prisoner’s actions are invisible. For each prisoner, the risk of a longer sentence is too great and the logical action is to agree to testify. Since this is true for both prisoners, though, if each follows their rational self-interest, both will be convicted on the major charge!
We can show it like this:
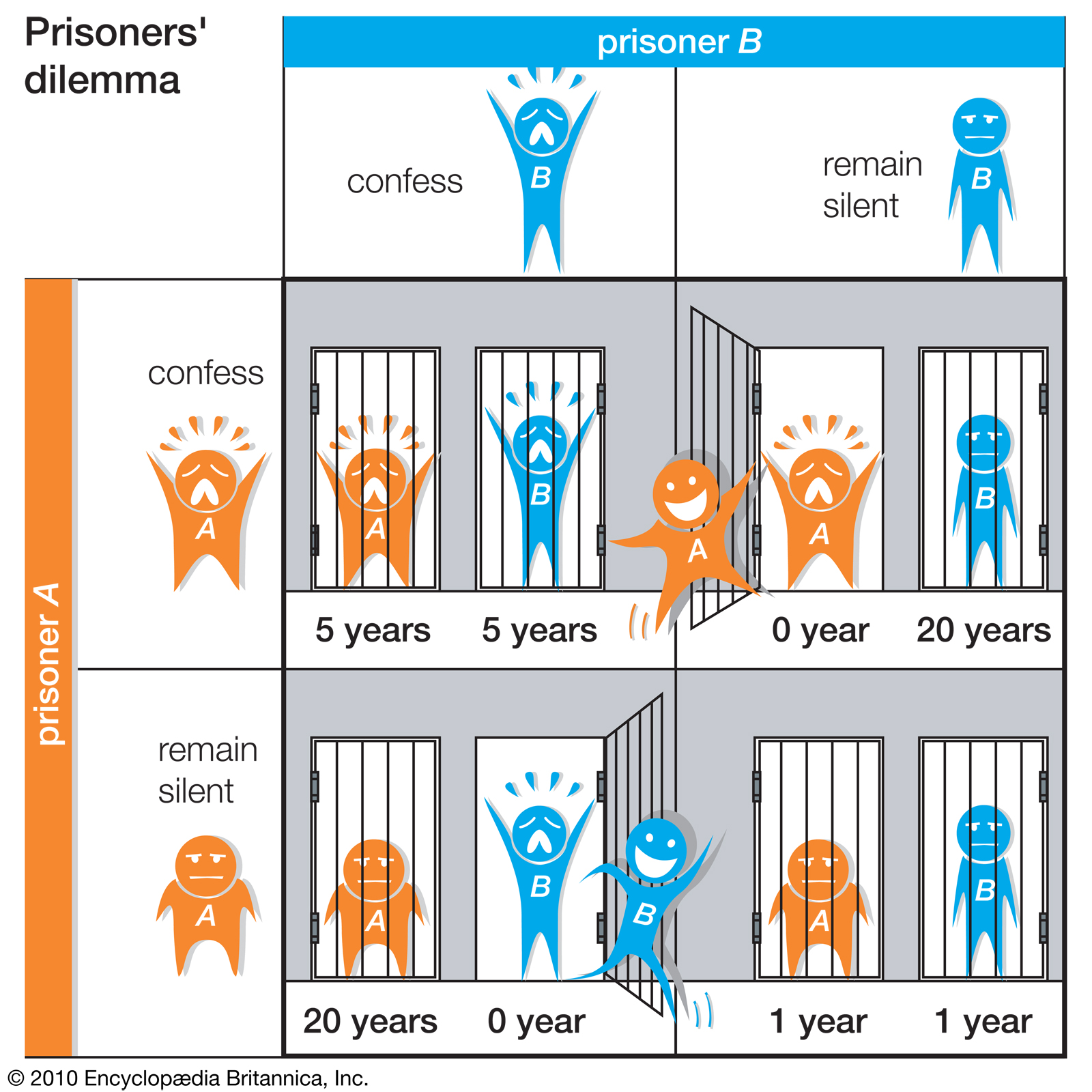
The prisoner’s dilemma illustrates some of the shortcomings of classical economics; where is the invisible hand? It also indicates the value of social trust.
High trust, low trust, and the iterative prisoner’s dilemma
There’s an iterative version of the prisoner’s dilemma game that allows participants to go through the process several times. In some, the number of iterations is known to the participants; in others, it isn’t. In all cases, the participants would be best off if they acted as if they had already agreed to remain silent and kept their word. If they act in a “classically rational” manner, the result is a spiral of retaliation without end.
If you replace “defect” (the technical term for “agree to testify”) with some other negative outcome and expand the number of players massively, you have a reasonable model of how human societies might behave.
The prisoner’s dilemma also lets us model social trust. I and my neighbor are both better off if we honor our debts to each other and respect each other’s property. But I can make a quick profit by stealing his car. In a world without police, this temptation is difficult for all to resist, not least for those without cars themselves. So people group together for mutual protection, fortify their property, hire security, and preemptively attack those whom they think might attack them. The resulting world is much poorer and more violent, with much effort wasted. This is a low-trust society.
Again, replace a few words and this describes international relations, at least before the modern era. (It also describes an era of history that explains the fortified houses of Italian renaissance cities.)
A high-trust society is one in which I and my neighbor so fully expect each other to behave well that we don’t bother to fortify our homes, carry weapons, or plot and scheme against each other. High-trust societies are distinguished by general prosperity and low crime and corruption. I don’t need to divert productive energy to watching my back, or waste money on defenses. But if you behave as if you’re in a high-trust society when you’re actually in a low-trust one, you will become a victim.
The prisoner’s dilemma and its variants can tell us about a lot more than just two crooks in a jailhouse. (There’s more to game theory than the prisoner’s dilemma, too.)
Other types of game theory games: Dictators, centipedes, volunteers — and limitations
Other common types of game used to model behaviour are the dictator’s game, the centipede game and the volunteer’s game.
The Dictator game
Less sinister than it sounds at first, this game lets one player decide how to split a prize with the other player. Only the first player has any input into the decision. It’s a very simple game, but it shows the importance of attaching accountability to asset control. (About 50% of players simply keep the money; about 45% allocate a smaller share to the other player. Only around 5% of players split the prize equally.)
The centipede game
The centipede game is similar to the prisoner’s dilemma, with the important difference that it’s about mutually allocating benefits rather than costs. Two or more players control a stash of money which they can choose to pass on to the other person, or to take immediately. If they take it, they get the larger share and the other player(s) get a smaller share. If they pass it on instead, it grows, increasing both the eventual reward and the likelihood that they will receive a smaller share of that reward. Again, this is a way to model social trust and help build understandings of how people and entities will behave in similar circumstances — as when oligopolies are both competing for market dominance, and cooperating to grow their market.
The volunteer’s dilemma
The volunteer’s dilemma is familiar if you had housemates in college. Players have to volunteer for chores. The worst possible outcome for all is if no-one volunteers, and no chores get done. But each player is motivated to avoid the worst or most unpleasant chores. This doesn’t just model the reason why the sink is full of dishes in the dorm, though. It gives us insight into the forces at play when onlookers don’t whistleblow on financial fraud or other kinds of wrongdoing — they’d be volunteering for negative consequences for themselves for the common good.
Nash equilibrium
A Nash equilibrium occurs when players in a game theory game like the prisoner’s dilemma can achieve their objectives by not deviating from their initial strategy. For instance, if you’re playing prisoner’s dilemma, your Nash equilibrium might be: “always defect”. It’s similar to an evolutionarily stable strategy.
Limitations of game theory
Game theory can offer insights, but it also has limitations. It makes the assumption that participants are rational and self-interested, which people are — but not all people, and not all the time. Individuals and entities, from participants in game theory-based psychological studies to major corporations and nation states, are influenced by other considerations and don’t always weigh every decision rationally.
Game theory also tends to assume a lack of context. In fact, there’s often a background of assumptions, prior knowledge and fairly reliable guesswork about others’ motivations, plans and motivations in play.
Game theory and digital assets
The digital assets marketplace can be modeled using game theory. For instance, the BTC market can be described in terms of two types of investors, Hodlers and Opportunists. Hodlers are operating at or near their maximum risk exposure; they have already bought as many BTC as they feel comfortable with and are likely to hang onto them long term. Opportunists may be newcomers to the BTC market, or they may be investors looking for short/medium-term gains.
In general, Hodlers will buy during low-volatility periods. Opportunists will end such periods and trigger volatility when they enter the market. Thus, each type of investor has two strategies they can use, depending on the behaviour of the other type of investor. All are acting in their own interests, competing for asymmetric rewards while cooperating to grow the overall value of BTC — a perfect application for game theory.
